Evolutionary Tools¶
The tools module contains the operators for evolutionary
algorithms. They are used to modify, select and move the individuals in their
environment. The set of operators it contains are readily usable in the
Toolbox. In addition to the basic operators this module
also contains utility tools to enhance the basic algorithms with
Statistics, HallOfFame, and History.
Operators¶
The operator set does the minimum job for transforming or selecting
individuals. This means, for example, that providing two individuals to the
crossover will transform those individuals in-place. The responsibility of
making offspring(s) independent of their parent(s) and invalidating the
fitness is left to the user and is generally fulfilled in the algorithms by
calling toolbox.clone() on an individual to duplicate it and
del on the values attribute of the individual’s fitness to
invalidate it.
Here is a list of the implemented operators in DEAP,
and genetic programming specific operators.
| Initialization | Crossover | Mutation | Bloat control |
|---|---|---|---|
genFull() |
cxOnePoint() |
mutShrink() |
staticLimit() |
genGrow() |
cxOnePointLeafBiased() |
mutUniform() |
selDoubleTournament() |
genHalfAndHalf() |
cxSemantic() |
mutNodeReplacement() |
|
mutEphemeral() |
|||
mutInsert() |
|||
mutSemantic() |
Initialization¶
-
deap.tools.initRepeat(container, func, n)[source]¶ Call the function func n times and return the results in a container type container
Parameters: - container – The type to put in the data from func.
- func – The function that will be called n times to fill the container.
- n – The number of times to repeat func.
Returns: An instance of the container filled with data from func.
This helper function can be used in conjunction with a Toolbox to register a generator of filled containers, as individuals or population.
>>> import random >>> random.seed(42) >>> initRepeat(list, random.random, 2) # doctest: +ELLIPSIS, ... # doctest: +NORMALIZE_WHITESPACE [0.6394..., 0.0250...]
See the List of Floats and Population tutorials for more examples.
-
deap.tools.initIterate(container, generator)[source]¶ Call the function container with an iterable as its only argument. The iterable must be returned by the method or the object generator.
Parameters: - container – The type to put in the data from func.
- generator – A function returning an iterable (list, tuple, …), the content of this iterable will fill the container.
Returns: An instance of the container filled with data from the generator.
This helper function can be used in conjunction with a Toolbox to register a generator of filled containers, as individuals or population.
>>> import random >>> from functools import partial >>> random.seed(42) >>> gen_idx = partial(random.sample, range(10), 10) >>> initIterate(list, gen_idx) # doctest: +SKIP [1, 0, 4, 9, 6, 5, 8, 2, 3, 7]
See the Permutation and Arithmetic Expression tutorials for more examples.
-
deap.tools.initCycle(container, seq_func, n=1)[source]¶ Call the function container with a generator function corresponding to the calling n times the functions present in seq_func.
Parameters: - container – The type to put in the data from func.
- seq_func – A list of function objects to be called in order to fill the container.
- n – Number of times to iterate through the list of functions.
Returns: An instance of the container filled with data from the returned by the functions.
This helper function can be used in conjunction with a Toolbox to register a generator of filled containers, as individuals or population.
>>> func_seq = [lambda:1 , lambda:'a', lambda:3] >>> initCycle(list, func_seq, n=2) [1, 'a', 3, 1, 'a', 3]
See the A Funky One tutorial for an example.
-
deap.gp.genFull(pset, min_, max_, type_=None)[source]¶ Generate an expression where each leaf has the same depth between min and max.
Parameters: - pset – Primitive set from which primitives are selected.
- min – Minimum height of the produced trees.
- max – Maximum Height of the produced trees.
- type – The type that should return the tree when called, when
None(default) the type of :pset: (pset.ret) is assumed.
Returns: A full tree with all leaves at the same depth.
-
deap.gp.genGrow(pset, min_, max_, type_=None)[source]¶ Generate an expression where each leaf might have a different depth between min and max.
Parameters: - pset – Primitive set from which primitives are selected.
- min – Minimum height of the produced trees.
- max – Maximum Height of the produced trees.
- type – The type that should return the tree when called, when
None(default) the type of :pset: (pset.ret) is assumed.
Returns: A grown tree with leaves at possibly different depths.
-
deap.gp.genHalfAndHalf(pset, min_, max_, type_=None)[source]¶ Generate an expression with a PrimitiveSet pset. Half the time, the expression is generated with
genGrow(), the other half, the expression is generated withgenFull().Parameters: - pset – Primitive set from which primitives are selected.
- min – Minimum height of the produced trees.
- max – Maximum Height of the produced trees.
- type – The type that should return the tree when called, when
None(default) the type of :pset: (pset.ret) is assumed.
Returns: Either, a full or a grown tree.
-
deap.gp.genRamped(pset, min_, max_, type_=None)[source]¶ Deprecated since version 1.0: The function has been renamed. Use
genHalfAndHalf()instead.
Crossover¶
-
deap.tools.cxOnePoint(ind1, ind2)[source]¶ Executes a one point crossover on the input sequence individuals. The two individuals are modified in place. The resulting individuals will respectively have the length of the other.
Parameters: - ind1 – The first individual participating in the crossover.
- ind2 – The second individual participating in the crossover.
Returns: A tuple of two individuals.
This function uses the
randint()function from the python baserandommodule.
-
deap.tools.cxTwoPoint(ind1, ind2)[source]¶ Executes a two-point crossover on the input sequence individuals. The two individuals are modified in place and both keep their original length.
Parameters: - ind1 – The first individual participating in the crossover.
- ind2 – The second individual participating in the crossover.
Returns: A tuple of two individuals.
This function uses the
randint()function from the Python baserandommodule.
-
deap.tools.cxTwoPoints(ind1, ind2)[source]¶ Deprecated since version 1.0: The function has been renamed. Use
cxTwoPoint()instead.
-
deap.tools.cxUniform(ind1, ind2, indpb)[source]¶ Executes a uniform crossover that modify in place the two sequence individuals. The attributes are swapped according to the indpb probability.
Parameters: - ind1 – The first individual participating in the crossover.
- ind2 – The second individual participating in the crossover.
- indpb – Independent probability for each attribute to be exchanged.
Returns: A tuple of two individuals.
This function uses the
random()function from the python baserandommodule.
-
deap.tools.cxPartialyMatched(ind1, ind2)[source]¶ Executes a partially matched crossover (PMX) on the input individuals. The two individuals are modified in place. This crossover expects sequence individuals of indices, the result for any other type of individuals is unpredictable.
Parameters: - ind1 – The first individual participating in the crossover.
- ind2 – The second individual participating in the crossover.
Returns: A tuple of two individuals.
Moreover, this crossover generates two children by matching pairs of values in a certain range of the two parents and swapping the values of those indexes. For more details see [Goldberg1985].
This function uses the
randint()function from the python baserandommodule.[Goldberg1985] Goldberg and Lingel, “Alleles, loci, and the traveling salesman problem”, 1985.
-
deap.tools.cxUniformPartialyMatched(ind1, ind2, indpb)[source]¶ Executes a uniform partially matched crossover (UPMX) on the input individuals. The two individuals are modified in place. This crossover expects sequence individuals of indices, the result for any other type of individuals is unpredictable.
Parameters: - ind1 – The first individual participating in the crossover.
- ind2 – The second individual participating in the crossover.
Returns: A tuple of two individuals.
Moreover, this crossover generates two children by matching pairs of values chosen at random with a probability of indpb in the two parents and swapping the values of those indexes. For more details see [Cicirello2000].
This function uses the
random()andrandint()functions from the python baserandommodule.[Cicirello2000] Cicirello and Smith, “Modeling GA performance for control parameter optimization”, 2000.
-
deap.tools.cxOrdered(ind1, ind2)[source]¶ Executes an ordered crossover (OX) on the input individuals. The two individuals are modified in place. This crossover expects sequence individuals of indices, the result for any other type of individuals is unpredictable.
Parameters: - ind1 – The first individual participating in the crossover.
- ind2 – The second individual participating in the crossover.
Returns: A tuple of two individuals.
Moreover, this crossover generates holes in the input individuals. A hole is created when an attribute of an individual is between the two crossover points of the other individual. Then it rotates the element so that all holes are between the crossover points and fills them with the removed elements in order. For more details see [Goldberg1989].
This function uses the
sample()function from the python baserandommodule.[Goldberg1989] Goldberg. Genetic algorithms in search, optimization and machine learning. Addison Wesley, 1989
-
deap.tools.cxBlend(ind1, ind2, alpha)[source]¶ Executes a blend crossover that modify in-place the input individuals. The blend crossover expects sequence individuals of floating point numbers.
Parameters: - ind1 – The first individual participating in the crossover.
- ind2 – The second individual participating in the crossover.
- alpha – Extent of the interval in which the new values can be drawn for each attribute on both side of the parents’ attributes.
Returns: A tuple of two individuals.
This function uses the
random()function from the python baserandommodule.
-
deap.tools.cxESBlend(ind1, ind2, alpha)[source]¶ Executes a blend crossover on both, the individual and the strategy. The individuals shall be a sequence and must have a sequence
strategyattribute. Adjustment of the minimal strategy shall be done after the call to this function, consider using a decorator.Parameters: - ind1 – The first evolution strategy participating in the crossover.
- ind2 – The second evolution strategy participating in the crossover.
- alpha – Extent of the interval in which the new values can be drawn for each attribute on both side of the parents’ attributes.
Returns: A tuple of two evolution strategies.
This function uses the
random()function from the python baserandommodule.
-
deap.tools.cxESTwoPoint(ind1, ind2)[source]¶ Executes a classical two points crossover on both the individuals and their strategy. The individuals shall be a sequence and must have a sequence
strategyattribute. The crossover points for the individual and the strategy are the same.Parameters: - ind1 – The first evolution strategy participating in the crossover.
- ind2 – The second evolution strategy participating in the crossover.
Returns: A tuple of two evolution strategies.
This function uses the
randint()function from the python baserandommodule.
-
deap.tools.cxESTwoPoints(ind1, ind2)[source]¶ Deprecated since version 1.0: The function has been renamed. Use
cxESTwoPoint()instead.
-
deap.tools.cxSimulatedBinary(ind1, ind2, eta)[source]¶ Executes a simulated binary crossover that modify in-place the input individuals. The simulated binary crossover expects sequence individuals of floating point numbers.
Parameters: - ind1 – The first individual participating in the crossover.
- ind2 – The second individual participating in the crossover.
- eta – Crowding degree of the crossover. A high eta will produce children resembling to their parents, while a small eta will produce solutions much more different.
Returns: A tuple of two individuals.
This function uses the
random()function from the python baserandommodule.
-
deap.tools.cxSimulatedBinaryBounded(ind1, ind2, eta, low, up)[source]¶ Executes a simulated binary crossover that modify in-place the input individuals. The simulated binary crossover expects sequence individuals of floating point numbers.
Parameters: - ind1 – The first individual participating in the crossover.
- ind2 – The second individual participating in the crossover.
- eta – Crowding degree of the crossover. A high eta will produce children resembling to their parents, while a small eta will produce solutions much more different.
- low – A value or a sequence of values that is the lower bound of the search space.
- up – A value or a sequence of values that is the upper bound of the search space.
Returns: A tuple of two individuals.
This function uses the
random()function from the python baserandommodule.Note
This implementation is similar to the one implemented in the original NSGA-II C code presented by Deb.
-
deap.tools.cxMessyOnePoint(ind1, ind2)[source]¶ Executes a one point crossover on sequence individual. The crossover will in most cases change the individuals size. The two individuals are modified in place.
Parameters: - ind1 – The first individual participating in the crossover.
- ind2 – The second individual participating in the crossover.
Returns: A tuple of two individuals.
This function uses the
randint()function from the python baserandommodule.
-
deap.gp.cxOnePoint(ind1, ind2)[source]¶ Randomly select crossover point in each individual and exchange each subtree with the point as root between each individual.
Parameters: - ind1 – First tree participating in the crossover.
- ind2 – Second tree participating in the crossover.
Returns: A tuple of two trees.
-
deap.gp.cxOnePointLeafBiased(ind1, ind2, termpb)[source]¶ Randomly select crossover point in each individual and exchange each subtree with the point as root between each individual.
Parameters: - ind1 – First typed tree participating in the crossover.
- ind2 – Second typed tree participating in the crossover.
- termpb – The probability of choosing a terminal node (leaf).
Returns: A tuple of two typed trees.
When the nodes are strongly typed, the operator makes sure the second node type corresponds to the first node type.
The parameter termpb sets the probability to choose between a terminal or non-terminal crossover point. For instance, as defined by Koza, non- terminal primitives are selected for 90% of the crossover points, and terminals for 10%, so termpb should be set to 0.1.
-
deap.gp.cxSemantic(ind1, ind2, gen_func=<function genGrow>, pset=None, min=2, max=6)[source]¶ Implementation of the Semantic Crossover operator [Geometric semantic genetic programming, Moraglio et al., 2012] offspring1 = random_tree1 * ind1 + (1 - random_tree1) * ind2 offspring2 = random_tree1 * ind2 + (1 - random_tree1) * ind1
Parameters: - ind1 – first parent
- ind2 – second parent
- gen_func – function responsible for the generation of the random tree that will be used during the mutation
- pset – Primitive Set, which contains terminal and operands to be used during the evolution
- min – min depth of the random tree
- max – max depth of the random tree
Returns: offsprings
The mutated offspring contains parents
>>> import operator >>> def lf(x): return 1 / (1 + math.exp(-x)); >>> pset = PrimitiveSet("main", 2) >>> pset.addPrimitive(operator.sub, 2) >>> pset.addTerminal(3) >>> pset.addPrimitive(lf, 1, name="lf") >>> pset.addPrimitive(operator.add, 2) >>> pset.addPrimitive(operator.mul, 2) >>> ind1 = genGrow(pset, 1, 3) >>> ind2 = genGrow(pset, 1, 3) >>> new_ind1, new_ind2 = cxSemantic(ind1, ind2, pset=pset, max=2) >>> ctr = sum([n.name == ind1[i].name for i, n in enumerate(new_ind1)]) >>> ctr == len(ind1) True >>> ctr = sum([n.name == ind2[i].name for i, n in enumerate(new_ind2)]) >>> ctr == len(ind2) True
Mutation¶
-
deap.tools.mutGaussian(individual, mu, sigma, indpb)[source]¶ This function applies a gaussian mutation of mean mu and standard deviation sigma on the input individual. This mutation expects a sequence individual composed of real valued attributes. The indpb argument is the probability of each attribute to be mutated.
Parameters: Returns: A tuple of one individual.
This function uses the
random()andgauss()functions from the python baserandommodule.
-
deap.tools.mutShuffleIndexes(individual, indpb)[source]¶ Shuffle the attributes of the input individual and return the mutant. The individual is expected to be a sequence. The indpb argument is the probability of each attribute to be moved. Usually this mutation is applied on vector of indices.
Parameters: - individual – Individual to be mutated.
- indpb – Independent probability for each attribute to be exchanged to another position.
Returns: A tuple of one individual.
This function uses the
random()andrandint()functions from the python baserandommodule.
-
deap.tools.mutFlipBit(individual, indpb)[source]¶ Flip the value of the attributes of the input individual and return the mutant. The individual is expected to be a sequence and the values of the attributes shall stay valid after the
notoperator is called on them. The indpb argument is the probability of each attribute to be flipped. This mutation is usually applied on boolean individuals.Parameters: - individual – Individual to be mutated.
- indpb – Independent probability for each attribute to be flipped.
Returns: A tuple of one individual.
This function uses the
random()function from the python baserandommodule.
-
deap.tools.mutUniformInt(individual, low, up, indpb)[source]¶ Mutate an individual by replacing attributes, with probability indpb, by a integer uniformly drawn between low and up inclusively.
Parameters: - individual – Sequence individual to be mutated.
- low – The lower bound or a sequence of of lower bounds of the range from which to draw the new integer.
- up – The upper bound or a sequence of of upper bounds of the range from which to draw the new integer.
- indpb – Independent probability for each attribute to be mutated.
Returns: A tuple of one individual.
-
deap.tools.mutPolynomialBounded(individual, eta, low, up, indpb)[source]¶ Polynomial mutation as implemented in original NSGA-II algorithm in C by Deb.
Parameters: - individual – Sequence individual to be mutated.
- eta – Crowding degree of the mutation. A high eta will produce a mutant resembling its parent, while a small eta will produce a solution much more different.
- low – A value or a sequence of values that is the lower bound of the search space.
- up – A value or a sequence of values that is the upper bound of the search space.
- indpb – Independent probability for each attribute to be mutated.
Returns: A tuple of one individual.
-
deap.tools.mutESLogNormal(individual, c, indpb)[source]¶ Mutate an evolution strategy according to its
strategyattribute as described in [Beyer2002]. First the strategy is mutated according to an extended log normal rule, \(\\boldsymbol{\sigma}_t = \\exp(\\tau_0 \mathcal{N}_0(0, 1)) \\left[ \\sigma_{t-1, 1}\\exp(\\tau \mathcal{N}_1(0, 1)), \ldots, \\sigma_{t-1, n} \\exp(\\tau \mathcal{N}_n(0, 1))\\right]\), with \(\\tau_0 = \\frac{c}{\\sqrt{2n}}\) and \(\\tau = \\frac{c}{\\sqrt{2\\sqrt{n}}}\), the the individual is mutated by a normal distribution of mean 0 and standard deviation of \(\\boldsymbol{\sigma}_{t}\) (its current strategy) then . A recommended choice isc=1when using a \((10, 100)\) evolution strategy [Beyer2002] [Schwefel1995].Parameters: - individual – Sequence individual to be mutated.
- c – The learning parameter.
- indpb – Independent probability for each attribute to be mutated.
Returns: A tuple of one individual.
[Beyer2002] (1, 2) Beyer and Schwefel, 2002, Evolution strategies - A Comprehensive Introduction [Schwefel1995] Schwefel, 1995, Evolution and Optimum Seeking. Wiley, New York, NY
-
deap.gp.mutShrink(individual)[source]¶ This operator shrinks the individual by choosing randomly a branch and replacing it with one of the branch’s arguments (also randomly chosen).
Parameters: individual – The tree to be shrunk. Returns: A tuple of one tree.
-
deap.gp.mutUniform(individual, expr, pset)[source]¶ Randomly select a point in the tree individual, then replace the subtree at that point as a root by the expression generated using method
expr().Parameters: - individual – The tree to be mutated.
- expr – A function object that can generate an expression when called.
Returns: A tuple of one tree.
-
deap.gp.mutNodeReplacement(individual, pset)[source]¶ Replaces a randomly chosen primitive from individual by a randomly chosen primitive with the same number of arguments from the
psetattribute of the individual.Parameters: individual – The normal or typed tree to be mutated. Returns: A tuple of one tree.
-
deap.gp.mutEphemeral(individual, mode)[source]¶ This operator works on the constants of the tree individual. In mode
"one", it will change the value of one of the individual ephemeral constants by calling its generator function. In mode"all", it will change the value of all the ephemeral constants.Parameters: - individual – The normal or typed tree to be mutated.
- mode – A string to indicate to change
"one"or"all"ephemeral constants.
Returns: A tuple of one tree.
-
deap.gp.mutInsert(individual, pset)[source]¶ Inserts a new branch at a random position in individual. The subtree at the chosen position is used as child node of the created subtree, in that way, it is really an insertion rather than a replacement. Note that the original subtree will become one of the children of the new primitive inserted, but not perforce the first (its position is randomly selected if the new primitive has more than one child).
Parameters: individual – The normal or typed tree to be mutated. Returns: A tuple of one tree.
-
deap.gp.mutSemantic(individual, gen_func=<function genGrow>, pset=None, ms=None, min=2, max=6)[source]¶ Implementation of the Semantic Mutation operator. [Geometric semantic genetic programming, Moraglio et al., 2012] mutated_individual = individual + logistic * (random_tree1 - random_tree2)
Parameters: - individual – individual to mutate
- gen_func – function responsible for the generation of the random tree that will be used during the mutation
- pset – Primitive Set, which contains terminal and operands to be used during the evolution
- ms – Mutation Step
- min – min depth of the random tree
- max – max depth of the random tree
Returns: mutated individual
The mutated contains the original individual
>>> import operator >>> def lf(x): return 1 / (1 + math.exp(-x)); >>> pset = PrimitiveSet("main", 2) >>> pset.addPrimitive(operator.sub, 2) >>> pset.addTerminal(3) >>> pset.addPrimitive(lf, 1, name="lf") >>> pset.addPrimitive(operator.add, 2) >>> pset.addPrimitive(operator.mul, 2) >>> individual = genGrow(pset, 1, 3) >>> mutated = mutSemantic(individual, pset=pset, max=2) >>> ctr = sum([m.name == individual[i].name for i, m in enumerate(mutated[0])]) >>> ctr == len(individual) True
Selection¶
-
deap.tools.selTournament(individuals, k, tournsize, fit_attr='fitness')[source]¶ Select the best individual among tournsize randomly chosen individuals, k times. The list returned contains references to the input individuals.
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
- tournsize – The number of individuals participating in each tournament.
- fit_attr – The attribute of individuals to use as selection criterion
Returns: A list of selected individuals.
This function uses the
choice()function from the python baserandommodule.
-
deap.tools.selRoulette(individuals, k, fit_attr='fitness')[source]¶ Select k individuals from the input individuals using k spins of a roulette. The selection is made by looking only at the first objective of each individual. The list returned contains references to the input individuals.
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
- fit_attr – The attribute of individuals to use as selection criterion
Returns: A list of selected individuals.
This function uses the
random()function from the python baserandommodule.Warning
The roulette selection by definition cannot be used for minimization or when the fitness can be smaller or equal to 0.
-
deap.tools.selNSGA2(individuals, k, nd='standard')[source]¶ Apply NSGA-II selection operator on the individuals. Usually, the size of individuals will be larger than k because any individual present in individuals will appear in the returned list at most once. Having the size of individuals equals to k will have no effect other than sorting the population according to their front rank. The list returned contains references to the input individuals. For more details on the NSGA-II operator see [Deb2002].
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
- nd – Specify the non-dominated algorithm to use: ‘standard’ or ‘log’.
Returns: A list of selected individuals.
[Deb2002] Deb, Pratab, Agarwal, and Meyarivan, “A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II”, 2002.
-
deap.tools.selNSGA3(individuals, k, ref_points, nd='log', best_point=None, worst_point=None, extreme_points=None, return_memory=False)[source]¶ Implementation of NSGA-III selection as presented in [Deb2014].
This implementation is partly based on lmarti/nsgaiii. It departs slightly from the original implementation in that it does not use memory to keep track of ideal and extreme points. This choice has been made to fit the functional api of DEAP. For a version of NSGA-III see
selNSGA3WithMemory.Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
- ref_points – Reference points to use for niching.
- nd – Specify the non-dominated algorithm to use: ‘standard’ or ‘log’.
- best_point – Best point found at previous generation. If not provided find the best point only from current individuals.
- worst_point – Worst point found at previous generation. If not provided find the worst point only from current individuals.
- extreme_points – Extreme points found at previous generation. If not provided find the extreme points only from current individuals.
- return_memory – If
True, return the best, worst and extreme points in addition to the chosen individuals.
Returns: A list of selected individuals.
Returns: If return_memory is
True, a namedtuple with the best_point, worst_point, and extreme_points.You can generate the reference points using the
uniform_reference_points()function:>>> ref_points = tools.uniform_reference_points(nobj=3, p=12) >>> selected = selNSGA3(population, k, ref_points)
[Deb2014] Deb, K., & Jain, H. (2014). An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Transactions on Evolutionary Computation, 18(4), 577-601. doi:10.1109/TEVC.2013.2281535.
-
deap.tools.selNSGA3WithMemory(ref_points, nd='log')[source]¶ Class version of NSGA-III selection including memory for best, worst and extreme points. Registering this operator in a toolbox is a bit different than classical operators, it requires to instantiate the class instead of just registering the function:
>>> from deap import base >>> ref_points = uniform_reference_points(nobj=3, p=12) >>> toolbox = base.Toolbox() >>> toolbox.register("select", selNSGA3WithMemory(ref_points))
-
deap.tools.uniform_reference_points(nobj, p=4, scaling=None)[source]¶ Generate reference points uniformly on the hyperplane intersecting each axis at 1. The scaling factor is used to combine multiple layers of reference points.
-
deap.tools.selSPEA2(individuals, k)[source]¶ Apply SPEA-II selection operator on the individuals. Usually, the size of individuals will be larger than n because any individual present in individuals will appear in the returned list at most once. Having the size of individuals equals to n will have no effect other than sorting the population according to a strength Pareto scheme. The list returned contains references to the input individuals. For more details on the SPEA-II operator see [Zitzler2001].
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
Returns: A list of selected individuals.
[Zitzler2001] Zitzler, Laumanns and Thiele, “SPEA 2: Improving the strength Pareto evolutionary algorithm”, 2001.
-
deap.tools.selRandom(individuals, k)[source]¶ Select k individuals at random from the input individuals with replacement. The list returned contains references to the input individuals.
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
Returns: A list of selected individuals.
This function uses the
choice()function from the python baserandommodule.
-
deap.tools.selBest(individuals, k, fit_attr='fitness')[source]¶ Select the k best individuals among the input individuals. The list returned contains references to the input individuals.
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
- fit_attr – The attribute of individuals to use as selection criterion
Returns: A list containing the k best individuals.
-
deap.tools.selWorst(individuals, k, fit_attr='fitness')[source]¶ Select the k worst individuals among the input individuals. The list returned contains references to the input individuals.
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
- fit_attr – The attribute of individuals to use as selection criterion
Returns: A list containing the k worst individuals.
-
deap.tools.selDoubleTournament(individuals, k, fitness_size, parsimony_size, fitness_first, fit_attr='fitness')[source]¶ Tournament selection which use the size of the individuals in order to discriminate good solutions. This kind of tournament is obviously useless with fixed-length representation, but has been shown to significantly reduce excessive growth of individuals, especially in GP, where it can be used as a bloat control technique (see [Luke2002fighting]). This selection operator implements the double tournament technique presented in this paper.
The core principle is to use a normal tournament selection, but using a special sample function to select aspirants, which is another tournament based on the size of the individuals. To ensure that the selection pressure is not too high, the size of the size tournament (the number of candidates evaluated) can be a real number between 1 and 2. In this case, the smaller individual among two will be selected with a probability size_tourn_size/2. For instance, if size_tourn_size is set to 1.4, then the smaller individual will have a 0.7 probability to be selected.
Note
In GP, it has been shown that this operator produces better results when it is combined with some kind of a depth limit.
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
- fitness_size – The number of individuals participating in each fitness tournament
- parsimony_size – The number of individuals participating in each size tournament. This value has to be a real number in the range [1,2], see above for details.
- fitness_first – Set this to True if the first tournament done should be the fitness one (i.e. the fitness tournament producing aspirants for the size tournament). Setting it to False will behaves as the opposite (size tournament feeding fitness tournaments with candidates). It has been shown that this parameter does not have a significant effect in most cases (see [Luke2002fighting]).
- fit_attr – The attribute of individuals to use as selection criterion
Returns: A list of selected individuals.
[Luke2002fighting] (1, 2) Luke and Panait, 2002, Fighting bloat with nonparametric parsimony pressure
-
deap.tools.selStochasticUniversalSampling(individuals, k, fit_attr='fitness')[source]¶ Select the k individuals among the input individuals. The selection is made by using a single random value to sample all of the individuals by choosing them at evenly spaced intervals. The list returned contains references to the input individuals.
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
- fit_attr – The attribute of individuals to use as selection criterion
Returns: A list of selected individuals.
This function uses the
uniform()function from the python baserandommodule.
-
deap.tools.selTournamentDCD(individuals, k)[source]¶ Tournament selection based on dominance (D) between two individuals, if the two individuals do not interdominate the selection is made based on crowding distance (CD). The individuals sequence length has to be a multiple of 4 only if k is equal to the length of individuals. Starting from the beginning of the selected individuals, two consecutive individuals will be different (assuming all individuals in the input list are unique). Each individual from the input list won’t be selected more than twice.
This selection requires the individuals to have a
crowding_distattribute, which can be set by theassignCrowdingDist()function.Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select. Must be less than or equal to len(individuals).
Returns: A list of selected individuals.
-
deap.tools.selLexicase(individuals, k)[source]¶ Returns an individual that does the best on the fitness cases when considered one at a time in random order. http://faculty.hampshire.edu/lspector/pubs/lexicase-IEEE-TEC.pdf
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
Returns: A list of selected individuals.
-
deap.tools.selEpsilonLexicase(individuals, k, epsilon)[source]¶ Returns an individual that does the best on the fitness cases when considered one at a time in random order. Requires a epsilon parameter. https://push-language.hampshire.edu/uploads/default/original/1X/35c30e47ef6323a0a949402914453f277fb1b5b0.pdf Implemented epsilon_y implementation.
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
Returns: A list of selected individuals.
-
deap.tools.selAutomaticEpsilonLexicase(individuals, k)[source]¶ Returns an individual that does the best on the fitness cases when considered one at a time in random order. https://push-language.hampshire.edu/uploads/default/original/1X/35c30e47ef6323a0a949402914453f277fb1b5b0.pdf Implemented lambda_epsilon_y implementation.
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
Returns: A list of selected individuals.
-
deap.tools.sortNondominated(individuals, k, first_front_only=False)[source]¶ Sort the first k individuals into different nondomination levels using the “Fast Nondominated Sorting Approach” proposed by Deb et al., see [Deb2002]. This algorithm has a time complexity of \(O(MN^2)\), where \(M\) is the number of objectives and \(N\) the number of individuals.
Parameters: - individuals – A list of individuals to select from.
- k – The number of individuals to select.
- first_front_only – If
Truesort only the first front and exit.
Returns: A list of Pareto fronts (lists), the first list includes nondominated individuals.
[Deb2002] Deb, Pratab, Agarwal, and Meyarivan, “A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II”, 2002.
-
deap.tools.sortLogNondominated(individuals, k, first_front_only=False)[source]¶ Sort individuals in pareto non-dominated fronts using the Generalized Reduced Run-Time Complexity Non-Dominated Sorting Algorithm presented by Fortin et al. (2013).
Parameters: individuals – A list of individuals to select from. Returns: A list of Pareto fronts (lists), with the first list being the true Pareto front.
Bloat control¶
-
deap.gp.staticLimit(key, max_value)[source]¶ Implement a static limit on some measurement on a GP tree, as defined by Koza in [Koza1989]. It may be used to decorate both crossover and mutation operators. When an invalid (over the limit) child is generated, it is simply replaced by one of its parents, randomly selected.
This operator can be used to avoid memory errors occurring when the tree gets higher than 90 levels (as Python puts a limit on the call stack depth), because it can ensure that no tree higher than this limit will ever be accepted in the population, except if it was generated at initialization time.
Parameters: - key – The function to use in order the get the wanted value. For
instance, on a GP tree,
operator.attrgetter('height')may be used to set a depth limit, andlento set a size limit. - max_value – The maximum value allowed for the given measurement.
Returns: A decorator that can be applied to a GP operator using
decorate()Note
If you want to reproduce the exact behavior intended by Koza, set key to
operator.attrgetter('height')and max_value to 17.[Koza1989] J.R. Koza, Genetic Programming - On the Programming of Computers by Means of Natural Selection (MIT Press, Cambridge, MA, 1992) - key – The function to use in order the get the wanted value. For
instance, on a GP tree,
Migration¶
-
deap.tools.migRing(populations, k, selection[, replacement, migarray])[source]¶ Perform a ring migration between the populations. The migration first select k emigrants from each population using the specified selection operator and then replace k individuals from the associated population in the migarray by the emigrants. If no replacement operator is specified, the immigrants will replace the emigrants of the population, otherwise, the immigrants will replace the individuals selected by the replacement operator. The migration array, if provided, shall contain each population’s index once and only once. If no migration array is provided, it defaults to a serial ring migration (1 – 2 – … – n – 1). Selection and replacement function are called using the signature
selection(populations[i], k)andreplacement(populations[i], k). It is important to note that the replacement strategy must select k different individuals. For example, using a traditional tournament for replacement strategy will thus give undesirable effects, two individuals will most likely try to enter the same slot.Parameters: - populations – A list of (sub-)populations on which to operate migration.
- k – The number of individuals to migrate.
- selection – The function to use for selection.
- replacement – The function to use to select which individuals will
be replaced. If
None(default) the individuals that leave the population are directly replaced. - migarray – A list of indices indicating where the individuals from a particular position in the list goes. This defaults to a ring migration.
Statistics¶
-
class
deap.tools.Statistics([key])[source]¶ Object that compiles statistics on a list of arbitrary objects. When created the statistics object receives a key argument that is used to get the values on which the function will be computed. If not provided the key argument defaults to the identity function.
The value returned by the key may be a multi-dimensional object, i.e.: a tuple or a list, as long as the statistical function registered support it. So for example, statistics can be computed directly on multi-objective fitnesses when using numpy statistical function.
Parameters: key – A function to access the values on which to compute the statistics, optional. >>> import numpy >>> s = Statistics() >>> s.register("mean", numpy.mean) >>> s.register("max", max) >>> s.compile([1, 2, 3, 4]) {'max': 4, 'mean': 2.5} >>> s.compile([5, 6, 7, 8]) {'mean': 6.5, 'max': 8}
-
compile(data)[source]¶ Apply to the input sequence data each registered function and return the results as a dictionary.
Parameters: data – Sequence of objects on which the statistics are computed.
-
register(name, function, *args, **kargs)[source]¶ Register a function that will be applied on the sequence each time
record()is called.Parameters: - name – The name of the statistics function as it would appear in the dictionary of the statistics object.
- function – A function that will compute the desired statistics on the data as preprocessed by the key.
- argument – One or more argument (and keyword argument) to pass automatically to the registered function when called, optional.
-
-
class
deap.tools.MultiStatistics(**kargs)[source]¶ Dictionary of
Statisticsobject allowing to compute statistics on multiple keys using a single call tocompile(). It takes a set of key-value pairs associating a statistics object to a unique name. This name can then be used to retrieve the statistics object.The following code computes statistics simultaneously on the length and the first value of the provided objects.
>>> from operator import itemgetter >>> import numpy >>> len_stats = Statistics(key=len) >>> itm0_stats = Statistics(key=itemgetter(0)) >>> mstats = MultiStatistics(length=len_stats, item=itm0_stats) >>> mstats.register("mean", numpy.mean, axis=0) >>> mstats.register("max", numpy.max, axis=0) >>> mstats.compile([[0.0, 1.0, 1.0, 5.0], [2.0, 5.0]]) {'length': {'mean': 3.0, 'max': 4}, 'item': {'mean': 1.0, 'max': 2.0}}
-
compile(data)[source]¶ Calls
Statistics.compile()with data of eachStatisticsobject.Parameters: data – Sequence of objects on which the statistics are computed.
-
register(name, function, *args, **kargs)[source]¶ Register a function in each
Statisticsobject.Parameters: - name – The name of the statistics function as it would appear in the dictionary of the statistics object.
- function – A function that will compute the desired statistics on the data as preprocessed by the key.
- argument – One or more argument (and keyword argument) to pass automatically to the registered function when called, optional.
-
Logbook¶
-
class
deap.tools.Logbook[source]¶ Evolution records as a chronological list of dictionaries.
Data can be retrieved via the
select()method given the appropriate names.The
Logbookclass may also contain other logbooks referred to as chapters. Chapters are used to store information associated to a specific part of the evolution. For example when computing statistics on different components of individuals (namelyMultiStatistics), chapters can be used to distinguish the average fitness and the average size.-
chapters= None¶ Dictionary containing the sub-sections of the logbook which are also
Logbook. Chapters are automatically created when the right hand side of a keyworded argument, provided to the record function, is a dictionary. The keyword determines the chapter’s name. For example, the following line adds a new chapter “size” that will contain the fields “max” and “mean”.logbook.record(gen=0, size={'max' : 10.0, 'mean' : 7.5})
To access a specific chapter, use the name of the chapter as a dictionary key. For example, to access the size chapter and select the mean use
logbook.chapters["size"].select("mean")
Compiling a
MultiStatisticsobject returns a dictionary containing dictionaries, therefore when recording such an object in a logbook using the keyword argument unpacking operator (**), chapters will be automatically added to the logbook.>>> fit_stats = Statistics(key=attrgetter("fitness.values")) >>> size_stats = Statistics(key=len) >>> mstats = MultiStatistics(fitness=fit_stats, size=size_stats) >>> # [...] >>> record = mstats.compile(population) >>> logbook.record(**record) >>> print logbook fitness length ------------ ------------ max mean max mean 2 1 4 3
-
header= None¶ Order of the columns to print when using the
streamand__str__()methods. The syntax is a single iterable containing string elements. For example, with the previously defined statistics class, one can print the generation and the fitness average, and maximum withlogbook.header = ("gen", "mean", "max")
If not set the header is built with all fields, in arbitrary order on insertion of the first data. The header can be removed by setting it to
None.
-
log_header= None¶ Tells the log book to output or not the header when streaming the first line or getting its entire string representation. This defaults
True.
-
pop(index=0)[source]¶ Retrieve and delete element index. The header and stream will be adjusted to follow the modification.
Parameters: item – The index of the element to remove, optional. It defaults to the first element. You can also use the following syntax to delete elements.
del log[0] del log[1::5]
-
record(**infos)[source]¶ Enter a record of event in the logbook as a list of key-value pairs. The information are appended chronologically to a list as a dictionary. When the value part of a pair is a dictionary, the information contained in the dictionary are recorded in a chapter entitled as the name of the key part of the pair. Chapters are also Logbook.
-
select(*names)[source]¶ Return a list of values associated to the names provided in argument in each dictionary of the Statistics object list. One list per name is returned in order.
>>> log = Logbook() >>> log.record(gen=0, mean=5.4, max=10.0) >>> log.record(gen=1, mean=9.4, max=15.0) >>> log.select("mean") [5.4, 9.4] >>> log.select("gen", "max") ([0, 1], [10.0, 15.0])
With a
MultiStatisticsobject, the statistics for each measurement can be retrieved using thechaptersmember :>>> log = Logbook() >>> log.record(**{'gen': 0, 'fit': {'mean': 0.8, 'max': 1.5}, ... 'size': {'mean': 25.4, 'max': 67}}) >>> log.record(**{'gen': 1, 'fit': {'mean': 0.95, 'max': 1.7}, ... 'size': {'mean': 28.1, 'max': 71}}) >>> log.chapters['size'].select("mean") [25.4, 28.1] >>> log.chapters['fit'].select("gen", "max") ([0, 1], [1.5, 1.7])
-
stream¶ Retrieve the formatted not streamed yet entries of the database including the headers.
>>> log = Logbook() >>> log.append({'gen' : 0}) >>> print log.stream gen 0 >>> log.append({'gen' : 1}) >>> print log.stream 1
-
Hall-Of-Fame¶
-
class
deap.tools.HallOfFame(maxsize, similar=<built-in function eq>)[source]¶ The hall of fame contains the best individual that ever lived in the population during the evolution. It is lexicographically sorted at all time so that the first element of the hall of fame is the individual that has the best first fitness value ever seen, according to the weights provided to the fitness at creation time.
The insertion is made so that old individuals have priority on new individuals. A single copy of each individual is kept at all time, the equivalence between two individuals is made by the operator passed to the similar argument.
Parameters: - maxsize – The maximum number of individual to keep in the hall of fame.
- similar – An equivalence operator between two individuals, optional.
It defaults to operator
operator.eq().
The class
HallOfFameprovides an interface similar to a list (without being one completely). It is possible to retrieve its length, to iterate on it forward and backward and to get an item or a slice from it.-
update(population)[source]¶ Update the hall of fame with the population by replacing the worst individuals in it by the best individuals present in population (if they are better). The size of the hall of fame is kept constant.
Parameters: population – A list of individual with a fitness attribute to update the hall of fame with.
-
insert(item)[source]¶ Insert a new individual in the hall of fame using the
bisect_right()function. The inserted individual is inserted on the right side of an equal individual. Inserting a new individual in the hall of fame also preserve the hall of fame’s order. This method does not check for the size of the hall of fame, in a way that inserting a new individual in a full hall of fame will not remove the worst individual to maintain a constant size.Parameters: item – The individual with a fitness attribute to insert in the hall of fame.
-
class
deap.tools.ParetoFront([similar])[source]¶ The Pareto front hall of fame contains all the non-dominated individuals that ever lived in the population. That means that the Pareto front hall of fame can contain an infinity of different individuals.
Parameters: similar – A function that tells the Pareto front whether or not two individuals are similar, optional. The size of the front may become very large if it is used for example on a continuous function with a continuous domain. In order to limit the number of individuals, it is possible to specify a similarity function that will return
Trueif the genotype of two individuals are similar. In that case only one of the two individuals will be added to the hall of fame. By default the similarity function isoperator.eq().Since, the Pareto front hall of fame inherits from the
HallOfFame, it is sorted lexicographically at every moment.-
update(population)[source]¶ Update the Pareto front hall of fame with the population by adding the individuals from the population that are not dominated by the hall of fame. If any individual in the hall of fame is dominated it is removed.
Parameters: population – A list of individual with a fitness attribute to update the hall of fame with.
-
History¶
-
class
deap.tools.History[source]¶ The
Historyclass helps to build a genealogy of all the individuals produced in the evolution. It contains two attributes, thegenealogy_treethat is a dictionary of lists indexed by individual, the list contain the indices of the parents. The second attributegenealogy_historycontains every individual indexed by their individual number as in the genealogy tree.The produced genealogy tree is compatible with NetworkX, here is how to plot the genealogy tree
history = History() # Decorate the variation operators toolbox.decorate("mate", history.decorator) toolbox.decorate("mutate", history.decorator) # Create the population and populate the history population = toolbox.population(n=POPSIZE) history.update(population) # Do the evolution, the decorators will take care of updating the # history # [...] import matplotlib.pyplot as plt import networkx graph = networkx.DiGraph(history.genealogy_tree) graph = graph.reverse() # Make the graph top-down colors = [toolbox.evaluate(history.genealogy_history[i])[0] for i in graph] networkx.draw(graph, node_color=colors) plt.show()
Using NetworkX in combination with pygraphviz (dot layout) this amazing genealogy tree can be obtained from the OneMax example with a population size of 20 and 5 generations, where the color of the nodes indicate their fitness, blue is low and red is high.
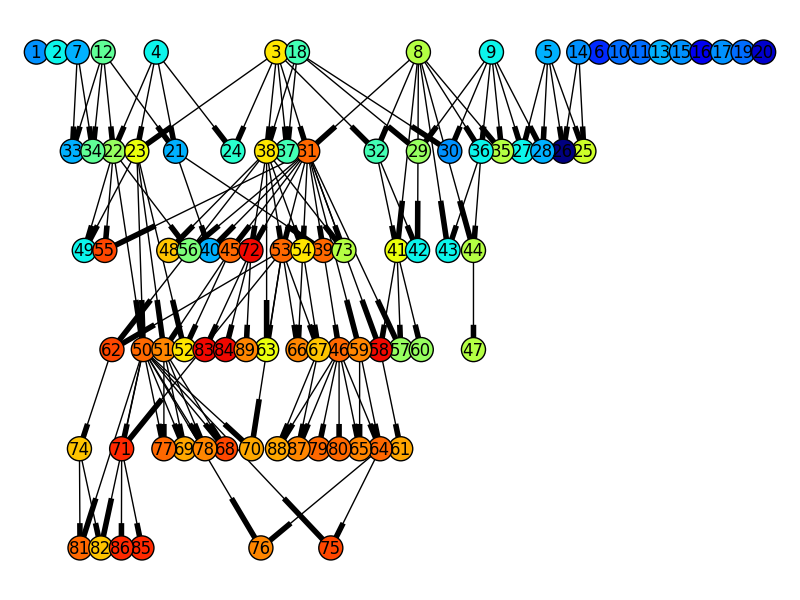
Note
The genealogy tree might get very big if your population and/or the number of generation is large.
-
update(individuals)[source]¶ Update the history with the new individuals. The index present in their
history_indexattribute will be used to locate their parents, it is then modified to a unique one to keep track of those new individuals. This method should be called on the individuals after each variation.Parameters: individuals – The list of modified individuals that shall be inserted in the history. If the individuals do not have a
history_indexattribute, the attribute is added and this individual is considered as having no parent. This method should be called with the initial population to initialize the history.Modifying the internal
genealogy_indexof the history or thehistory_indexof an individual may lead to unpredictable results and corruption of the history.
-
decorator¶ Property that returns an appropriate decorator to enhance the operators of the toolbox. The returned decorator assumes that the individuals are returned by the operator. First the decorator calls the underlying operation and then calls the
update()function with what has been returned by the operator. Finally, it returns the individuals with their history parameters modified according to the update function.
-
getGenealogy(individual[, max_depth])[source]¶ Provide the genealogy tree of an individual. The individual must have an attribute
history_indexas defined byupdate()in order to retrieve its associated genealogy tree. The returned graph contains the parents up to max_depth variations before this individual. If not provided the maximum depth is up to the beginning of the evolution.Parameters: - individual – The individual at the root of the genealogy tree.
- max_depth – The approximate maximum distance between the root (individual) and the leaves (parents), optional.
Returns: A dictionary where each key is an individual index and the values are a tuple corresponding to the index of the parents.
-
Constraints¶
-
class
deap.tools.DeltaPenalty(feasibility, delta[, distance])[source]¶ This decorator returns penalized fitness for invalid individuals and the original fitness value for valid individuals. The penalized fitness is made of a constant factor delta added with an (optional) distance penalty. The distance function, if provided, shall return a value growing as the individual moves away the valid zone.
Parameters: - feasibility – A function returning the validity status of any individual.
- delta – Constant or array of constants returned for an invalid individual.
- distance – A function returning the distance between the individual and a given valid point. The distance function can also return a sequence of length equal to the number of objectives to affect multi-objective fitnesses differently (optional, defaults to 0).
Returns: A decorator for evaluation function.
This function relies on the fitness weights to add correctly the distance. The fitness value of the ith objective is defined as
\[f^\mathrm{penalty}_i(\mathbf{x}) = \Delta_i - w_i d_i(\mathbf{x})\]where \(\mathbf{x}\) is the individual, \(\Delta_i\) is a user defined constant and \(w_i\) is the weight of the ith objective. \(\Delta\) should be worst than the fitness of any possible individual, this means higher than any fitness for minimization and lower than any fitness for maximization.
See the Constraint Handling for an example.
-
class
deap.tools.ClosestValidPenalty(feasibility, feasible, alpha[, distance])[source]¶ This decorator returns penalized fitness for invalid individuals and the original fitness value for valid individuals. The penalized fitness is made of the fitness of the closest valid individual added with a weighted (optional) distance penalty. The distance function, if provided, shall return a value growing as the individual moves away the valid zone.
Parameters: - feasibility – A function returning the validity status of any individual.
- feasible – A function returning the closest feasible individual from the current invalid individual.
- alpha – Multiplication factor on the distance between the valid and invalid individual.
- distance – A function returning the distance between the individual and a given valid point. The distance function can also return a sequence of length equal to the number of objectives to affect multi-objective fitnesses differently (optional, defaults to 0).
Returns: A decorator for evaluation function.
This function relies on the fitness weights to add correctly the distance. The fitness value of the ith objective is defined as
\[\begin{split}f^\mathrm{penalty}_i(\mathbf{x}) = f_i(\operatorname{valid}(\mathbf{x})) - \\alpha w_i d_i(\operatorname{valid}(\mathbf{x}), \mathbf{x})\end{split}\]where \(\mathbf{x}\) is the individual, \(\operatorname{valid}(\mathbf{x})\) is a function returning the closest valid individual to \(\mathbf{x}\), \(\\alpha\) is the distance multiplicative factor and \(w_i\) is the weight of the ith objective.